Java 树结构的基础部分(一）

二叉树
1.1 为什么需要树这种数据结构
1) 数组存储方式的分析
优点：通过下标方式访问元素，速度快。对于有序数组，还可使用二分查找提高检索速度。
缺点：如果要检索具体某个值，或者插入值(按一定顺序)会整体移动，效率较低 [示意图]
画出操作示意图：
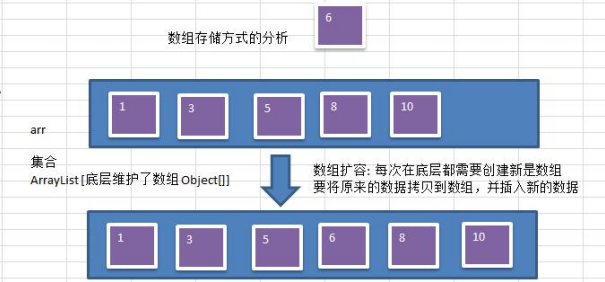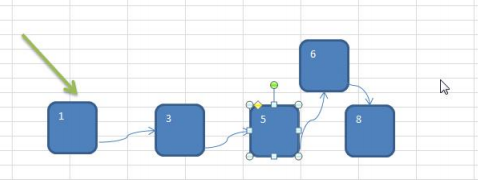
2) 链式存储方式的分析
优点：在一定程度上对数组存储方式有优化(比如：插入一个数值节点，只需要将插入节点，链接到链表中即可，
删除效率也很好)。
缺点：在进行检索时，效率仍然较低，比如(检索某个值，需要从头节点开始遍历) 【示意图】
操作示意图：
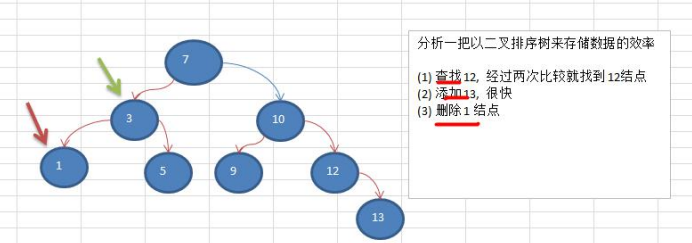
3) 树存储方式的分析
能提高数据存储，读取的效率, 比如利用 二叉排序树(Binary Sort Tree)，既可以保证数据的检索速度，同时也
可以保证数据的插入，删除，修改的速度。【示意图,后面详讲】
案例: [7, 3, 10, 1, 5, 9, 12] 

1.2 树示意图

 

树的常用术语(结合示意图理解):
1) 节点
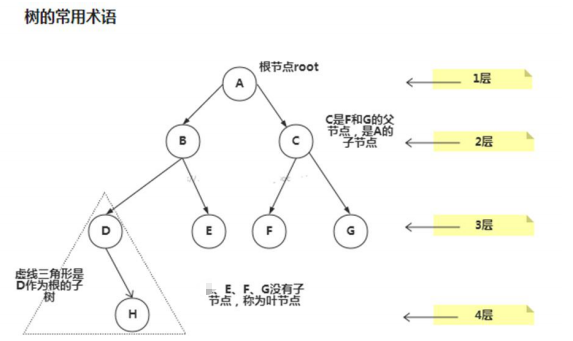
2) 根节点
3) 父节点
4) 子节点
5) 叶子节点 (没有子节点的节点)
6) 节点的权(节点值)
7) 路径(从 root 节点找到该节点的路线)
8) 层
9) 子树
10) 树的高度(最大层数)
11) 森林 :多颗子树构成森林
1.3 二叉树的概念
1) 树有很多种，每个节点最多只能有两个子节点的一种形式称为二叉树。
2) 二叉树的子节点分为左节点和右节点
3) 示意图 
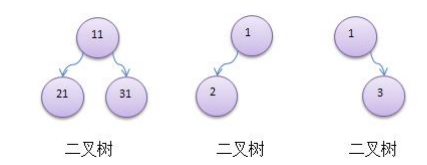4) 如果该二叉树的所有叶子节点都在最后一层，并且结点总数= 2^n -1 , n 为层数，则我们称为满二叉树。
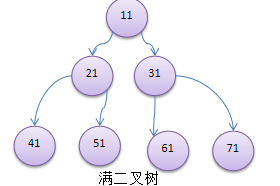5) 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二
层的叶子节点在右边连续，我们称为完全二叉树 
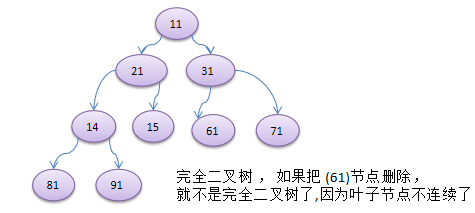1.4 二叉树遍历的说明
使用前序，中序和后序对下面的二叉树进行遍历.
1) 前序遍历: 先输出父节点，再遍历左子树和右子树
2) 中序遍历: 先遍历左子树，再输出父节点，再遍历右子树
3) 后序遍历: 先遍历左子树，再遍历右子树，最后输出父节点
4) 小结: 看输出父节点的顺序，就确定是前序，中序还是后序
1.5 二叉树遍历应用实例(前序,中序,后序)
　　应用实例的说明和思路 

　　 代码实现

 在最后面

1.6 二叉树-查找指定节点
要求
1) 请编写前序查找，中序查找和后序查找的方法。
2) 并分别使用三种查找方式，查找 heroNO = 5 的节点
3) 并分析各种查找方式，分别比较了多少次4) 思路分析图解

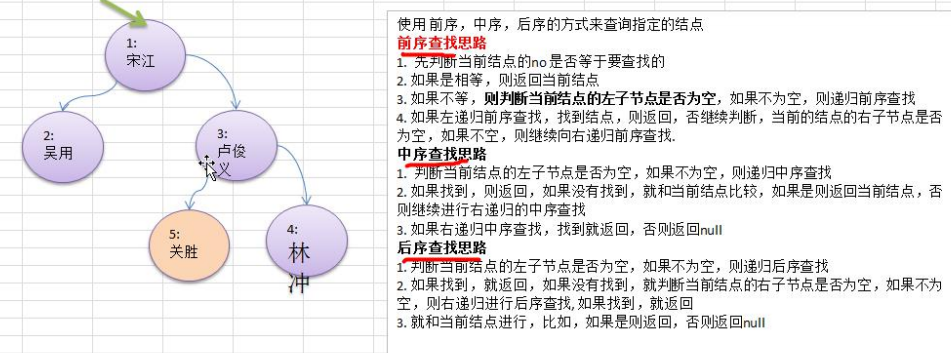5) 代码实现
在最后面
1.7 二叉树-删除节点
要求
1) 如果删除的节点是叶子节点，则删除该节点
2) 如果删除的节点是非叶子节点，则删除该子树
3) 测试，删除掉 5 号叶子节点 和 3 号子树.
4) 完成删除思路分析
5) 代码实现

package com.lin.tree_0308;public class BinaryTreeDemo { public static void main(String[] args) {    BinaryTree binaryTree = new BinaryTree();    HeroNode heroNode1 = new HeroNode(1, "伍六七");  HeroNode heroNode2 = new HeroNode(2, "梅花十一");  HeroNode heroNode3 = new HeroNode(3, "梅花十三");  HeroNode heroNode4 = new HeroNode(4, "江主任");  HeroNode heroNode5 = new HeroNode(5, "希义");    heroNode1.setLeft(heroNode2);  heroNode1.setRight(heroNode3);  heroNode3.setRight(heroNode4);  heroNode3.setLeft(heroNode5);  binaryTree.setRoot(heroNode1);  //  System.out.println("前序遍历：");//  binaryTree.preOrder();  //  System.out.println("中序遍历：");//  binaryTree.infixOrder();//  //  System.out.println("后序遍历");//  binaryTree.postOrder();  //  System.out.println("前序查找：");//  HeroNode preOrderSearch = binaryTree.preOrderSearch(5);//  if(preOrderSearch != null) {//   System.out.println(preOrderSearch);//  } else {//   System.out.println("没有找到");//  }  //  System.out.println("中序查找：");//  HeroNode infixOrderSearch = binaryTree.infixOrderSearch(5);//  if(infixOrderSearch != null) {//   System.out.println(infixOrderSearch);//  } else {//   System.out.println("没有找到");//  }//  //  System.out.println("后序查找：");//  HeroNode postOrderSearch = binaryTree.postOrderSearch(5);//  if(postOrderSearch != null) {//   System.out.println(postOrderSearch);//  } else {//   System.out.println("没有找到");//  }    System.out.println("删除前");  binaryTree.preOrder();    binaryTree.delNode(2);    System.out.println("删除后");  binaryTree.preOrder(); }}

 

class BinaryTree{ private HeroNode root; public void setRoot(HeroNode root) {  this.root = root; }  // 删除节点 public void delNode(int no) {  if (root != null) {   // 如果只有一个root   if (root.getNo() == no) {    root = null;   } else {    root.delNode(no);   }  } else {   System.out.println("空树！");  } }  // 前序遍历 public void preOrder() {  if(this.root != null) {   this.root.preOrder();  } else {   System.out.println("二叉树为空!");  } }  // 中序遍历 public void infixOrder() {  if(this.root != null) {   this.root.infixOrder();  } else {   System.out.println("二叉树为空！");  } }  // 后序遍历 public void postOrder() {  if(this.root != null) {   this.root.postOrder();  } else {   System.out.println("二叉树为空！");  } }  // 前序查找 public HeroNode preOrderSearch(int no) {  if(root != null) {   return root.preOrderSearch(no);  } else {   return null;  } } // 中序查找 public HeroNode infixOrderSearch(int no) {  if (root != null) {   return root.infixOrderSearch(no);  } else {   return null;  } } // 后序查找 public HeroNode postOrderSearch(int no) {  if (root != null) {   return root.postOrderSearch(no);  } else {   return null;  } }}

 

class HeroNode{ private String name; private int no; private HeroNode left; private HeroNode right;  public HeroNode(int no, String name) {  this.no = no;  this.name = name; }  public String getName() {  return name; } public void setName(String name) {  this.name = name; } public int getNo() {  return no; } public void setNo(int no) {  this.no = no; } public HeroNode getLeft() {  return left; } public void setLeft(HeroNode left) {  this.left = left; } public HeroNode getRight() {  return right; } public void setRight(HeroNode right) {  this.right = right; } @Override public String toString() {  return "HeroNode [name=" + name + ", no=" + no + "]"; }  // 前序遍历 public void preOrder() {  System.out.println(this); // 输出父节点  if(this.left != null) {   this.left.preOrder();  }  if(this.right != null) {   this.right.preOrder();  } }  // 中序遍历 public void infixOrder() {  if (this.left != null) {   this.left.infixOrder();  }  System.out.println(this); // 输出父节点  if (this.right != null) {   this.right.infixOrder();  } }   // 前序遍历 public void postOrder() {  if (this.left != null) {   this.left.postOrder();  }  if (this.right != null) {   this.right.postOrder();  }  System.out.println(this); // 输出父节点 }  // 前序查找 public HeroNode preOrderSearch(int no) {  System.out.println("1");  // 比较当前节点是不是  if(this.no == no) {   return this;  }  // 1 判断当前节点的左节点是否为空，如果不为空，则递归前序查找  // 2 如果左递归前序查找，找到节点，则返回  HeroNode resNode = null;  if(this.left != null) {   resNode = this.left.preOrderSearch(no);  }  if(resNode != null) {// 说明左子树找到了   return resNode;  }  // 1 左递归如果没有找到，则继续判断  // 2 当前节点的右节点是否为空，如果不为空，则继续向右递归前序查找  if(this.right != null) {   resNode = this.right.preOrderSearch(no);  }  // 这时候不管有没有找到都要返回resNode  return resNode;  }  // 中序查找 public HeroNode infixOrderSearch(int no) {    HeroNode resNode = null;  if(this.left != null) {   resNode = this.left.infixOrderSearch(no);  }  if(resNode != null) {   return resNode;  }  System.out.println("1");  if(this.no == no) {   return this;  }    if(this.right != null) {   resNode = this.right.infixOrderSearch(no);  }  return resNode; }  // 后序查找 public HeroNode postOrderSearch(int no) {    HeroNode resNode = null;  if(this.left != null) {   resNode = this.left.postOrderSearch(no);  }  if(resNode != null) {   return resNode;  }    if(this.right != null) {   resNode = this.right.postOrderSearch(no);  }  if(resNode != null) {   return resNode;  }  System.out.println("1");  if(this.no == no) {   return this;  }  // 如果都没有找到  return resNode; }  /**  *  * @Description:1 因为我们的二叉树是单向，所以我们是判断当前节点的子节点是否需要删除节点，而不是直接去判断当前节点是否需要删除节点。<br>  *     2 如果当前节点的左子节点不为空，并且左子节点就是要删除节点，就将this.left = null；并且就返回（结束递归删除） <br>  *     3 如果当前节点的右子节点不为空，并且右子节点就是要删除节点，就将this.right = null；并且就返回（结束递归删除） <br>  *     4 如果第2和第3都没有删除节点，那么我们就需要向左子树进行递归删除<br>  *     5 如果第4补也没有删除节点，则向右子树进行递归删除<br>  * @author LinZM  * @date 2021-3-8 15:17:32  * @version V1.8  */ public void delNode(int no) {  if(this.left != null && this.left.no == no) {   this.left = null;   return;  }    if(this.right != null && this.right.no == no) {   this.right = null;   return;  }    if(this.left != null) {   this.left.delNode(no);  }    if(this.right != null) {   this.right.delNode(no);  } }}

 

仅供参考，有错误还请指出！

有什么想法，评论区留言，互相指教指教。

觉得不错的可以点一下右边的推荐哟

原文转载：http://www.shaoqun.com/a/611582.html

跨境电商：https://www.ikjzd.com/

shopyy：https://www.ikjzd.com/w/1661

海豚村：https://www.ikjzd.com/w/1779

二叉树1.1为什么需要树这种数据结构1)数组存储方式的分析优点：通过下标方式访问元素，速度快。对于有序数组，还可使用二分查找提高检索速度。缺点：如果要检索具体某个值，或者插入值(按一定顺序)会整体移动，效率较低[示意图]画出操作示意图：2)链式存储方式的分析优点：在一定程度上对数组存储方式有优化(比如：插入一个数值节点，只需要将插入节点，链接到链表中即可，删除效率也很好)。缺点：在进行检索时，效率
立刻网：https://www.ikjzd.com/w/2323
trax：https://www.ikjzd.com/w/1489
拍拍网服装：https://www.ikjzd.com/w/2205
亚马逊运营QA集锦（754-763）：https://www.ikjzd.com/home/124424
速卖通最新政策：3次严重侵权将被关闭账号！：https://www.ikjzd.com/home/8064
Amazon文案设计：https://www.kjyunke.com/courses/380